1. Tiệm cận trong cấu trúc dữ liệu và giải thuật là gì?
Tiệm cận trong cấu trúc dữ liệu và giải thuật được sử dụng để phân tích và ước lượng thời gian chạy (Running Time) của một giải thuật. Khi một thuật toán được cài đặt, bước phân tích tiệm cận của thuật toán sẽ giúp ta có thể đánh giá được các trường hợp tốt, trường hợp xấu, và trường hợp trung bình của thuật toán đó.
Khi phân tích tiệm cận cho một thuật toán không có đầu vào (input) – khi đó thời gian chạy của thuật toán này sẽ là một thời gian cố định (giả sử là n) và thời gian để thuật toán này chạy sẽ là một hằng số không đổi.
Phân tích tiệm cận cũng đề cập đến việc ước lượng thời gian chạy của bất kỳ phép tính nào trong các bước tính toán. Giả sử thời gian chạy của phép tính ban đầu được biểu diễn qua hàm f(n), thời gian chạy của phép tính khác sẽ được biểu diễn qua hàm g(n2). Trong phép tính cả hai phéo tính trên, giả sử giá trị n thay đổi, điều này có nghĩa là thời gian chạy của phép tính đầu tiên sẽ tăng tuyến tính với sự tăng lên của n và thời gian chạy của phép tính thứ hai sẽ tăng theo hàm mũ khi n tăng lên. Nếu n là một số đủ nhỏ, thì thời gian chạy của 2 phép tính sẽ sấp sỉ với nhau.
Trong một giải thuật, người ta thường phân loại các thời gian chạy theo lượng thời gian cần thiết thông qua 3 loại chính dưới đây:
- Trường hợp tốt nhất: là thời gian nhỏ nhất cần thiết để chạy giải thuật.
- Trường hợp trung bình: là thời gian trung bình cần thiết để chạy giải thuật.
- Trường hợp xấu nhất: là thời gian tối đa cần thiết để chạy giải thuật.
2. Các ký hiệu tiệm cận trong Cấu trúc dữ liệu và giải thuật
Trong khi ước lượng thời gian chạy của một giải thuật, ta cần sử dụng và quy ước một số ký hiệu tiệm cận để thông qua ký hiệu đó để đánh giá thuật toán. Dưới đây là một số ký hiệu tiệm cận được sử dụng phổ biến trong việc ước lượng độ phức tạp thời gian chạy của một giải thuật:
- Ký hiệu: Ο Notation
- Ký hiệu: Ω Notation
- Ký hiệu: θ Notation
2.1 Ký hiệu O Notation trong Cấu trúc dữ liệu và giải thuật
Ο(n) là một cách để biểu diễn tiệm cận trên của thời gian chạy của một giải thuật. Qua đó, O(n) sẽ ước lượng độ phức tạp thời gian của giải thuật, trong trường hợp xấu nhất sẽ tương đương với số lượng thời gian chạy dài nhất cần thiết cho một giải thuật tính từ khi giải thuật được thực thi từ bắt đầu cho đến khi kết thúc. Đồ thị biểu diễn như sau:
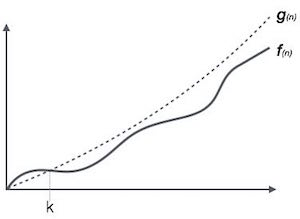
Giả sử ta có hai hàm f(n) và g(n) là các hàm tăng trong khoảng từ [0; +∞) khi đó tất cả các hàm thời gian đều thỏa mãn các điều kiện này:
Ο(f(n)) = { g(n) : nếu tồn tại c > 0 và n0 sao cho g(n) ≤ c.f(n) với mọi n > n0. }
2.2 Ký hiệu Ω Notation trong Cấu trúc dữ liệu và giải thuật
Ω(n) là một cách để biểu diễn tiệm cận dưới của thời gian chạy của một giải thuật. Qua đó, Ω(n) ước lượng độ phức tạp thời gian của giải thuật, trong trường hợp tốt nhất sẽ tương đương với số lượng thời gian chạy ngắn nhất cần thiết cho một giải thuật tính từ khi giải thuật được thực thi từ bắt đầu cho đến khi kết thúc. Đồ thị biểu diễn như sau:
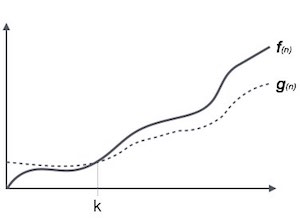
Giả sử ta có một hàm f(n) – khi đó:
Ω(f(n)) ≥ { g(n) : nếu tồn tại c > 0 và n0 sao cho g(n) ≤ c.f(n) với mọi n > n0. }
2.3 Ký hiệu θ Notation trong Cấu trúc dữ liệu và giải thuật
θ(n) là cách để biểu diễn cả tiệm cận trên và tiệm cận dưới của thời gian chạy của một giải thuật. Qua đó, θ(n) ước lượng độ phức tạp thời gian của giải thuật, trong trường hợp trung bình sẽ tương đương với số lượng thời gian chạy trung bình cần thiết cho một giải thuật tính từ khi giải thuật được thực thi từ bắt đầu cho đến khi kết thúc. Đồ thị biểu diễn như sau:
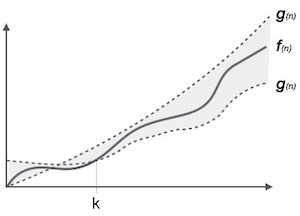
Giả sử ta có một hàm f(n) – khi đó:
θ(f(n)) = { g(n) nếu và chỉ nếu g(n) = Ο(f(n)) và g(n) = Ω(f(n)) với mọi n > n0. }
3. Một số ký hiệu tiệm cận phổ biến trong Cấu trúc dữ liệu và giải thuật
- Tiệm cận là hằng số – Ο(1)
- Tiệm cận logarit – Ο(log(n))
- Tiệm cận tuyến tính – Ο(n)
- Tiệm cận n*log(n) – Ο(n*log(n))
- Tiệm cận bậc hai – Ο(n2)
- Tiệm cận bậc 3 – Ο(n3)
- Tiệm cận đa thức – nΟ(1)
- Tiệm cận hàm mũ – 2Ο(n)


