1. Thuật toán tìm kiếm tuyến tính là gì?
Tìm kiếm tuyến tính hay còn được gọi là Tìm kiếm tuần tự là phương pháp chọn ra một phần tử được cho trước trong một danh sách (hoặc mảng) bằng cách duyệt lần lượt từng phần tử của danh sách đó cho đến lúc tìm thấy giá trị mong muốn cần tìm. Hoặc nếu đã duyệt qua toàn bộ lần lượt các phần tử trong danh sách mà không có bất kỳ phần tử nào trùng với phần tử cần tìm thì danh sách đó sẽ không chứa phần tử cần tìm kiếm.
Các bước thực hiện thuật toán tìm kiếm tuyến tính
Thuật toán tìm kiếm tuyến tính với Giá trị x cần tìm trong mảng A ban đầu: Bước 1: Thiết lập i thành 1 Bước 2: Nếu i > n thì chuyển tới bước 7 Bước 3: Nếu A[i] = x thì chuyển tới bước 6 Bước 4: Thiết lập i thành i + 1 Bước 5: Tới bước 2 Bước 6: In phần tử x được tìm thấy tại chỉ mục i và tới bước 8 Bước 7: In phần tử không được tìm thấy Bước 8: Thoát
Thuật toán tìm kiếm tuyến tính trong lập trình
Gọi hàm tìm kiếm tuyến tính linear_search(int A[], int n, int x)
for từng phần tử trong danh sách n phần tử của mảng A[]
if match item == x
return vị trí của phần tử
Kết thúc if
Kết thúc for
Kết thúc hàm
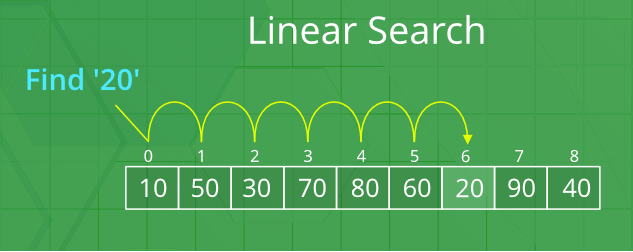
Hình ảnh minh họa dưới đây, cho chúng ta thấy một ví dụ đơn giản để sử dụng thuật toán tìm kiếm tuyến tính để tìm kiếm phần tử có giá trị 20 trong một mảng gồm nhiều phần tử như: [10, 50, 30, 70, 80, 60, 20, 90, 40]
2. Minh họa thuật toán tìm kiếm tuyến tính trong C
Khi sử dụng ngôn ngữ lập trình C, ta rất dễ dàng có thể cài đặt được thuật toán tìm kiếm tuyến tính cho một mảng. Bản chất việc tìm kiếm tuyến tính cũng chính là việc duyệt qua các phần tử có trong một mảng ban đầu và đem từng phần tử trong mảng đi so sánh với phần tử cần tìm kiếm. Để thuận tiện hơn cho việc cài đặt thuật toán tìm kiếm tuyến tính trong ngôn ngữ C, ta sẽ cần xây dựng 1 hàm có tên linear_search(int A[], int n, int x) – hàm này sẽ gồm 3 tham số:
- int A[] là mảng chứa các phần tử
- int n là số lượng phần tử có trong mảng int A[]
- int x là phần tử cần tìm trong int A[].
Hàm linear_search(int A[], int n, int x) được xây dựng như sau:
int linear_search(int A[], int n, int x){
int i;
for (i = 0; i < n; i++)
//Neu co phan tu A[i] nao co gia tri bang voi x
if (A[i] == x){
return i; //Tra ve vi tri phan tu duoc tim thay
}
return -1; //Khong tim thay phan tu trong mang A[]
}
Lưu ý: Hàm linear_search(int A[], int n, int x) sẽ trả về giá trị -1 nếu không tìm thấy phần tử nào trong mảng A[] và trong trường hợp nếu tìm thấy phần tử có giá trị nào trùng với giá trị của int x thì hàm sẽ trả về giá trị là vị trí i của phần tử được tìm thấy.
Chương trình đầy đủ về thuật toán tìm kiếm tuyến tính với mảng các số nguyên trong ngôn ngữ C như sau:
#include <stdio.h>
//Xay dung ham tim kiem tuyen tinh
int linear_search(int A[], int n, int x){
int i;
for (i = 0; i < n; i++)
//Neu co phan tu A[i] nao co gia tri bang voi x
if (A[i] == x){
return i; //Tra ve vi tri phan tu duoc tim thay
}
return -1; //Khong tim thay phan tu trong mang A[]
}
int main(){
//Khai bao bien n lam so luong phan tu mang
int n = 9;
//Khai bao mang gom cac phan tu
int A[n] = {10, 50, 30, 70, 80, 60, 20, 90, 40};
//Khai bao gia tri can tim trong mang A
int x = 20;
//Khai bao bien index de nhan ket qua tim kiem duoc tra ve tu ham linear_search(A,n,x)
int index = linear_search(A,n,x);
//Neu ket qua index bang -1
if(index == -1){
printf("Khong tim thay phan tu x = %d", x);
}else{ //Nguoc lai, neu index khong bang -1
printf("Tim thay x = %d tai vi tri %d", x, index);
}
}
Kết quả:
| Tim thay x = 20 tai vi tri 6 |
Giải thích:
- Đầu vào: A[] = {10, 50, 30, 70, 80, 60, 20, 90, 40}, n = 9, x = 20;
- Đầu ra: 6
- Kết quả: Phần tử x tồn tại ở chỉ số 6 của mảng A
Lưu ý: Các bạn có thể hoàn toàn thay đổi giá trị của biến int x hoặc thay đổi giá trị của mảng A[] để thực hiện lại việc tìm kiếm theo bài toán của riêng mình. Ở đây, tôi đã khai báo cứng cho một mảng A[] gồm 9 phần tử (n = 9) là {10, 50, 30, 70, 80, 60, 20, 90, 40 và giá trị x cần tìm trong A[] là 20.
3. Đánh giá thuật toán tìm kiếm tuyến tính
| Loại thuật toán: | Tìm kiếm phần tử |
| Thực hiện trong cấu trúc: | Danh sách, mảng |
| Độ phức tạp thời gian: | O(n) khi phần tử tìm kiếm nằm cuối danh sách hoặc không có trong danh sách |
| Thời gian chạy tốt nhất: | O(1) khi phần tử cần tìm nằm ngay đầu danh sách |
| Độ phức tạp không gian: | O(n) |


