Thao tác tìm kiếm là rất cần thiết trong việc thực hiện các thao tác như chèn, xóa hay sửa một phần tử có trong cây. Hay đơn giản chỉ là việc tìm kiếm và chọn ra phần tử phù hợp với một yêu cầu nào đó có trong cây! Trong cấu trúc cây khi thực hiện thao tác tìm kiếm ta có thể sử dụng theo 2 phương pháp đệ quy và không đệ quy.

1.Tìm kiếm phần tử trong cây theo phương pháp đệ quy

Với yêu cầu tìm kiếm một phần tử có dữ liệu x nào đó thuộc trong cây.

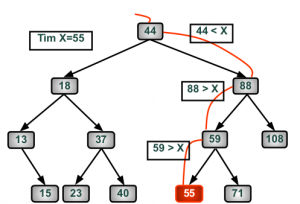
Đối với phương pháp tìm kiếm có sử dụng đệ quy ta cần thực hiện kiểm tra một số điều kiện sau đây:

• Nếu root->data == x, nghĩa là node gốc của cây có data bằng với x thì dừng việc tìm kiếm và return root; (Đây là điều kiện dừng của hàm tìm kiếm theo phương pháp đệ quy)
• Nếu root->data > x, nghĩa là node gốc của cây có data lớn hơn x thì ta sẽ thực hiện gọi đệ quy lại hàm tìm kiếm theo cây con trái
• Nếu root->data < x, nghĩa là node gốc của cây có data nhỏ hơn x thì ta sẽ thực hiện gọi đệ quy lại hàm tìm kiếm theo cây con phải

Để hiểu rõ hơn các bước trên, mời bạn đọc thêm đoạn code dưới đây:

Hàm SearchNodeRecursion(Tree root, int x) nhận tham số là node gốc của cây Tree root và int x là phần tử cần tìm kiếm:

Node* SearchNodeRecursion(Tree root, int x){
    //neu cay khong rong
    if(root!=NULL){
        //neu data cua node goc bang x can tim
        if(root->data == x){
            //tra ve node goc cua cay
            return root;
        }
        //neu data cua node goc lon hon x can tim  
        if(root->data > x){
            //goi lai ham tim kiem theo cay con trai
            return SearchNodeRecursion(root->left, x);
        }else{//nguoc lai data cua node goc nho hon x can tim
            //goi lai ham tim kiem theo cay con phai
            return SearchNodeRecursion(root->right, x);
        }
    }
    //neu khong tim thay node co data bang x thi tra ve rong
    return NULL;
}

2.Tìm kiếm phần tử trong cây không sử dụng đệ quy

Với yêu cần tìm một phần tử x với phương pháp tìm kiếm phần tử không sử dụng đệ quy việc tìm kiếm một phần tử chỉ đơn giản thực hiện các bước bên dưới đây:

• Dùng vòng lăp duyệt từ node gốc đến hết các node trong cây
• Trong vòng lặp kiểm tra điều kiện nếu tìm thấy node có dữ liệu bằng với x cần tìm thì trả về chính node đang được xét
• Nếu x < data của node đang xét trong vòng lặp thì để vòng lặp tiến theo cây con trái
• Ngược lại nếu x > data của node đang xét trong vòng lặp thì để vòng lặp tiến theo cây con phải

Mời bạn đọc cùng tham khảo đoạn code dưới đây để hiểu hơn về các bước trên.

Node* SearchNode(Tree root, int x){
    //tao va gan node p bang node goc
    Node *p = root;
    //duyet tu node goc den het cay
    while (p != NULL){
        //neu co data cua node p dang xet bang x can tim
        if(p->data==x){
            //tra ve node dang duoc xet
            return p;
        }else{
            //neu phan tu x can tim nho hon data cua node dang xet
            if(x < p->data){
                //tim kiem theo cay con trai
                p = p->left;
            }else{//nguoc lai neu phan tu x can tim lon hon data cua node dang xet
                //tim kiem theo cay con phai
                p = p->right;
            }
        }
    }
    //neu khong tim thay node co data bang x thi tra ve rong
    return NULL;
}

3.Chương trình tìm kiếm phần tử trong cây nhị phân hoàn chỉnh

Chương trình dưới đây sẽ là một chương trình hoàn chỉnh, sử dụng lại hai hàm tìm kiếm theo phương pháp đệ quy và không dùng đệ quy để tìm kiếm một phần từ x. Kết quả nhận được khi sử dụng cả hai hàm là giống nhau!

#include <stdio.h>
#include <stdlib.h>
typedef struct Node{
    //khai bao du lieu cua node co kieu du lieu int
    int data;
    //khai bao con tro den cay con trai
    Node* left;
    //khai bao con tro den cay con phai
    Node* right;

};
typedef struct Node* Tree;
Tree root;

void Init (Tree &root){   
    //gan node goc ve NULL
    root = NULL;
}

Node* CreateNode (int x){
    //tao node moi
    Node* p = new Node;
    //neu cay nhi phan khong rong
    if (p != NULL){
        //gan cay con trai va cay con phai mac dinh bang NULL
        p->left = NULL;
        p->right = NULL;
        //gan data bang x
        p->data = x;
    }
    //tra ve node p
    return p;
}
int InsertNode(Tree &root, Node*p){
    //neu node root khac rong thi thuc hien them vao cay
    if (root != NULL){
        //neu 2 data cua 2 node bang nhau thi ket thuc
        if (root->data==p->data){
            return 0;
        }
        //neu khoa cua root lon hon khoa cua p thi goi de quy trai 
        if (root->data > p->data){
            return InsertNode(root->left, p);
        }
        else{//neu khoa cua root nho hon khoa cua p thi goi de quy phai 
            return InsertNode(root->right,p);
        }
    }else { //truong hop neu node root la rong thi them node p vao node root
        root = p;
    }
}

void Input(Tree &root){
    int n;
    printf ("NHAP SO LUONG NODE CAN THEM: "); 
    scanf("%d",&n);
    for(int i=1; i<=n;i++){
        int x;
        printf ("NHAP DATA CUA NODE %d: ",i); 
        scanf("%d",&x);
        //tao node p co data = x
        Node* p = CreateNode(x);
        //them node p co data x vao trong cay
        InsertNode(root, p);
    }
}

void NLR(Tree root){
    if (root!=NULL){
        //hien thi du lieu cua tung node sau khi duyet
        printf("%d \t",root->data);
        //su dung de quy de duyet tiep cay con trai
        NLR(root->left);
        //su dung de quy de duyet tiep cay con phai
        NLR(root->right);
    }
}

Node* SearchNodeRecursion(Tree root, int x){
    //neu cay khong rong
    if(root!=NULL){
        //neu data cua node goc bang x can tim 
        if(root->data == x){
            //tra ve node goc cua cay
            return root;
        }
        //neu data cua node goc lon hon x can tim   
        if(root->data > x){
            //goi lai ham tim kiem theo cay con trai
            return SearchNodeRecursion(root->left, x);
        }else{//nguoc lai data cua node goc nho hon x can tim
            //goi lai ham tim kiem theo cay con phai 
            return SearchNodeRecursion(root->right, x);
        }
    }
    //neu khong tim thay node co data bang x thi tra ve rong
    return NULL;
}

Node* SearchNode(Tree root, int x){
    //tao va gan node p bang node goc
    Node *p = root;
    //duyet tu node goc den het cay
    while (p != NULL){
        //neu co data cua node p dang xet bang x can tim
        if(p->data==x){
            //tra ve node dang duoc xet
            return p;
        }else{
            //neu phan tu x can tim nho hon data cua node dang xet
            if(x < p->data){
                //tim kiem theo cay con trai
                p = p->left;
            }else{//nguoc lai neu phan tu x can tim lon hon data cua node dang xet
                //tim kiem theo cay con phai
                p = p->right;
            }
        }
    }
    //neu khong tim thay node co data bang x thi tra ve rong
    return NULL;
}

int main(){
    //tao cay voi node goc la root
    Tree root;
    //khoi tao cay
    Init(root);
    //nhap n phan tu vao cay
    Input(root);
    //duyet cay theo NLR
    printf("Duyet cay theo NLR\n");
    NLR(root);
    printf("\n");
    //tim kiem 
    int x = 5;
    //tim kiem theo ham co su dung de quy
    Node *p = SearchNodeRecursion(root,x);
    if(p == NULL){//neu node p la rong
        printf("Khong tim thay node");
    }else{
        printf("Tim thay phan tu %d theo phuong phap de quy", x);
    }
    printf("\n");
    //tim kiem theo ham khong dung de quy
    Node *k = SearchNode(root,x);
    if(k == NULL){ //neu node k la rong
        printf("Khong tim thay node");
    }else{
        printf("Tim thay phan tu %d khong dung de quy", x);
    }
}